Динамика вращательного движения. Динамика вращательного движения Связь величин, характеризующих поступательное и вращательное движение

Вот мальчик вращает камень на веревке. Он крутит этот камень все быстрее, пока веревка не оборвется. Тогда камень полетит куда-то в сторону. Какая же сила разорвала веревку? Ведь она удерживала камень, вес которого, конечно, не менялся. На веревку действует центробежная сила , отвечали ученые еще до . Еще задолго до Ньютона ученые выяснили, для того, чтобы тело вращалось, на него должна действовать сила. Но особенно хорошо это видно из законов Ньютона. Ньютон был первым ученым, . Он установил причину вращательного движения планет вокруг Солнца. Силой, вызывающей это движение, оказалась сила тяготения.

Центростремительная сила

Древнее оружие человека - праща

Центрирование ротора

Уравновешивание центробежных сил

При наблюдении сложных движений, например движения тела человека (ходьба, бег, прыжки и т.д.), кажется трудным или даже невозможным описать перемещение всех его точек. Однако, анализируя такие движения, можно заметить, что они состоят из более простых - поступательных и вращательных перемещений.

Механика поступательного движения известна читателю, поэтому раздел начинается с рассмотрения вращательного движения. Наиболее простым является вращение твердого тела вокруг неподвижной оси. Этот случай позволяет ознакомиться со спецификой, терминологией и законами вращательного движения.

5.1. КИНЕМАТИКА ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ АБСОЛЮТНО ТВЕРДОГО ТЕЛА ВОКРУГ НЕПОДВИЖНОЙ ОСИ

Абсолютно твердым телом называют такое, расстояние между любыми двумя точками которого неизменно.

Размеры и форма абсолютно твердого тела не изменяются при его движении.

Понятие «абсолютно твердое тело» - физическая абстракция, так как любое тело способно к деформациям. Однако во многих случаях деформацией можно пренебречь.

Наиболее простой случай вращательного движения абсолютно твердого тела - вращение относительно неподвижной оси. Это такое движение, при котором точки тела движутся по окружностям, центры которых лежат на прямой, называемой осью вращения.

Известно, что в некоторых случаях для характеристики движения тела необязательно указывать движение всех его точек; так, например, при поступательном движении достаточно указать движение любой одной точки тела.

При вращательном движении вокруг оси точки тела перемещаются по разным траекториям, но за одно и то же время все точки и само тело поворачивается на одинаковый угол. Для характеристики вращения

проведем в плоскости, перпендикулярной оси, радиус-вектор к некоторой точке i (рис. 5.1). Временная зависимость угла α поворота радиуса-вектора относительно некоторого выделенного направления ОХ является уравнением вращательного движения твердого тела вокруг неподвижной оси:

Быстрота вращения тела характеризуется угловой скоростью, равной первой производной от угла поворота радиуса-вектора по времени:

Угловая скорость есть вектор, который направлен по оси вращения и связан с направлением вращения правилом правого винта (рис. 5.2). Вектор угловой скорости в отличие от векторов скорости и силы является скользящим: у него нет определенной точки приложения, и он может быть расположен в любом месте на оси вращения. Таким образом, задание вектора ω указывает положение оси вращения, направление вращения и модуль угловой скорости.

Быстрота изменения угловой скорости характеризуется угловым ускорением, равным первой производной от угловой скорости по времени:

или в векторной форме:

Из (5.4) видно, что вектор углового ускорения совпадает по направлению с элементарным, достаточно малым изменением вектора угловой скорости dω : при ускоренном вращении угловое ускорение направлено так же, как и угловая скорость, при замедленном вращении - противоположно ей.

Так как угловое перемещение всех точек абсолютно твердого тела одинаково, то, согласно (5.2) и (5.3), одновременно все точки тела имеют одинаковую угловую скорость и одинаковое угловое ускорение. Линейные характеристики - перемещение, скорость, ускорение - различны для разных точек. Укажем в скалярном виде связь, которая может быть выведена самостоятельно, между линейными и угловыми характеристиками для i-й точки, движущейся по окружности радиусом r i:

Рис. 5.3

В заключение приведем полученные путем интегрирования соответствующих выражений формулы кинематики вращательного движения твердого тела вокруг неподвижной оси:

уравнение равномерного вращательного движения [см. (5.2)]:

зависимость угловой скорости от времени в равнопеременном вращательном движении [см. (5.3)]:

уравнение равнопеременного вращательного движения [см. (5.1) и (5.6)]:

Полезно сопоставить эти формулы с аналогичными зависимостями для поступательного движения.

5.2. ОСНОВНЫЕ ПОНЯТИЯ. УРАВНЕНИЕ ДИНАМИКИ ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ

Момент силы _

Пусть к некоторой точке i твердого тела приложена сила F^, лежащая в плоскости, перпендикулярной оси вращения (рис. 5.4).

Моментом силы относительно оси вращения называют векторное произведение радиуса-вектора точки i на силу:

Раскрывая его, можно записать:

где β - угол между векторами r i и F i . Так как плечо силы h i = r i sinβ (см. рис. 5.4), то

Если сила действует под некоторым углом α к плоскости вращения (рис. 5.5), то ее можно разложить на две составляющие. Одна из них лежит в плоскости, перпендикулярной оси вращения, а другая параллельна этой этой оси и не оказывает влияния на вращение тела (в реальном случае она действует лишь на подшипники). Далее будут рассматриваться только силы, лежащие в плоскости, перпендикулярной оси вращения.

Рис. 5.4

Рис. 5.5

Работа во вращательном движении

Пусть при действии силы F i (см. рис. 5.4) тело поворачивается на достаточно малый угол dα. Найдем работу этой силы.

Известное из средней школы выражение для работы силы в данном случае следует записать так:

Итак,

элементарная работа силы во вращательном движении равна произведению момента силы на элементарный угол поворота тела.

Если на тело действует несколько сил, то элементарная работа, совершенная всеми ими, определяется аналогично (5.12):

где М - суммарный момент всех внешних сил, действующих на тело.

Если при повороте тела положение радиуса-вектора изменилось от α 1 до α 2 , то работа внешних сил может быть найдена интегрированием выражения (5.13):

Момент инерции

Мерой инертности тел при поступательном движении является масса. Инертность тел при вращательном движении зависит не только от массы, но и от распределения ее в пространстве относительно оси. Мера инертности тела при вращении характеризуется моментом инерции тела относительно оси вращения. Укажем сначала, что

моментом инерции материальной точки относительно оси вращения называют величину, равную произведению массы точки на квадрат расстояния ее от оси:

Моментом инерции тела относительно оси называют сумму моментов инерции всех материальных точек, из которых состоит тело:

В качестве примера выведем формулу момента инерции тонкого однородного стержня длиной l и массой т относительно оси, перпендикулярной стержню и проходящей через его середину (рис. 5.6). Выберем достаточно малый участок стержня длиной dx и массой dm, удаленный от оси 00" на расстояние х. Ввиду малости этого участка он может быть принят за материальную точку, его момент инерции [см. (5.15)] равен:

Масса элементарного участка равна произведению линейной плотности т/l, умноженной на длину элементарного участка: dm = (m/l) dx Подставив это выражение в (5.18), получим

Чтобы найти момент инерции всего стержня, проинтегрируем выражение (5.19) по всему стержню, т.е. в пределах от -1/2 до +1/2:

Приведем выражения для моментов инерции разных симметричных тел массой т:

полого однородного цилиндра (обруча) с внутренним радиусом r и внешним R относительно оси ОО", совпадающей с геометрической осью цилиндра (рис. 5.7):

сплошного однородного цилиндра (r = 0) или диска [см. (5.21)]:

однородного шара относительно оси, проходящей через его центр:

прямоугольною параллелепипеда относительно оси ОО", проходящей через его центр перпендикулярно плоскости основания (рис. 5.8):

Во всех перечисленных примерах ось вращения проходит через центр масс тела. При решении задач для определения момента инерции тела относительно оси, не проходящей через центр масс, можно воспользоваться теоремой Гюйгенса. Согласно этой теореме, момент инерции тела относительно некоторой оси OO":

где J 0 - момент инерции относительно параллельной оси, проходящей через центр масс тела OO"; т - масса тела; d - расстояние между двумя параллельными осями (рис. 5.9). Единицей момента инерции является килограмм-метр в квадрате (кг-м 2).

Момент импульса

Моментом импульса (момент количества движения) материальной точки, вращающейся относительно некоторой оси, называется величина, равная произведению импульса точки на расстоянии ее до оси вращения:

Момент импульса тела, вращающегося относительно некоторой оси, равен сумме моментов импульсов точек, из которых состоит данное тело:

Так как угловая скорость всех точек твердого тела одинакова, выне-ся ω за знак суммы [см. (5.29)], получим:

(/ - момент инерции тела относительно оси), или в векторной форме:

Итак, момент импульса равен произведению момента инерции точки на угловую скорость. Отсюда следует, что направления векторов момента импульса и угловой скорости совпадают. Единицей момента импульса является килограмм-метр в квадрате в секунду (кг? м 2 ? с -1).

Формулу (5.31) полезно сравнить с аналогичной формулой для импульса в поступательном движении.

Кинетическая энергия вращающегося тела

При вращении тела его кинетическая энергия складывается из кинетических энергий отдельных точек тела. Для твердого тела:

Полезно сопоставить выражение (5.32) с аналогичным выражением для поступательного движения.

Продифференцировав (5.32), получим элементарное изменение кинетической энергии во вращательном движении:

Основное уравнение динамики вращательного движения

Пусть твердое тело, на которое действовали внешние силы, повернулось на достаточно малый угол da. Приравняем элементарную работу всех внешних сил при таком повороте [см. (5.13)] элементарному изменению кинетической энергии [см. (5.33)]: M dα = J ω dω , откуда:

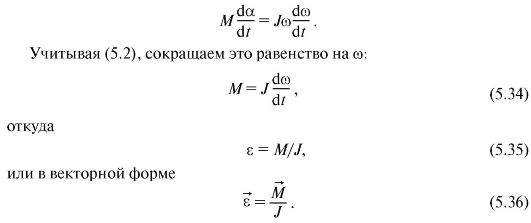
Это и есть основное уравнение динамики вращательного движения. Из (5.35) видно, что момент инерции характеризует инерционные свойства тела во вращательном движении: при действии внешних сил угловое ускорение тела тем больше, чем меньше момент инерции тела.

Основное уравнение для вращательного движения играет ту же роль, что и второй закон Ньютона для поступательного. Физические величины, входящие в это уравнение, аналогичны соответственно силе, массе и ускорению.

Из (5.34) следует, что:

Производная от момента импульса тела по времени равна равнодействующему моменту всех внешних сил.

Зависимость углового ускорения от момента силы и момента инерции можно продемонстрировать с по-

мощью прибора, изображенного на рис. 5.10. Под действием груза 1, подвешенного на нити, перекинутой через блок, крестовина ускоренно вращается. Перемещая грузики 2 на разные расстояния от оси вращения, можно изменять момент инерции крестовины. Меняя грузы, т.е. моменты сил, и момент инерции, можно убедиться, что угловое ускорение возрастает при увеличении момента силы или уменьшении момента инерции.

5.3. ЗАКОН СОХРАНЕНИЯ МОМЕНТА ИМПУЛЬСА

Рассмотрим частный случай вращательного движения, когда суммарный момент внешних сил равен нулю. Как видно из (5.37), dL/dt = 0 при М = 0, откуда

Это положение известно под названием закона сохранения момента импульса: если суммарный момент всех внешних сил, действующих на тело, равен нулю, то момент импульса этою тела остается постоянным.

Опуская доказательство, отметим, что закон сохранения момента импульса справедлив не только для абсолютно твердого тела.

Наиболее интересные применения этого закона связаны с вращением системы тел вокруг общей оси. При этом необходимо учитывать векторный характер момента импульса и угловых скоростей. Так, для системы, состоящей из N тел, вращающихся вокруг общей оси, закон сохранения момента импульса можно записать в форме:

Рассмотрим некоторые примеры, иллюстрирующие этот закон.

Гимнаст, выполняющий сальто (рис. 5.11), в начальной фазе сгибает колени и прижимает их к груди, уменьшая тем самым момент инерции и увеличивая угловую скорость вращения вокруг горизонтальной оси, проходящей через центр масс. В конце прыжка тело выпрямляется, момент инерции возрастает, угловая скорость уменьшается. Фигурист, совершающий вращение вокруг вертикальной оси (рис. 5.12), в начале вращения приближает руки к корпусу, тем самым уменьшая момент инерции и увеличивая угловую скорость. В конце вращения происходит обратный процесс: при разведении рук увеличивается момент инерции и уменьшается угловая скорость, что позволяет легко остановиться.

Такое же явление может быть продемонстрировано на скамье Жуковского, которая представляет собой легкую горизонтальную платформу, вращающуюся с малым трением вокруг вертикальной оси. При изменении положения рук изменяются момент инерции и угловая скорость (рис. 5.13), момент импульса остается постоянным. Для усиления демонстрационного эффекта в руках человека гантели. На скамье Жуковского можно продемонстрировать векторный характер закона сохранения момента импульса.

Экспериментатор, стоящий на неподвижной скамье, получает от помощника велосипедное колесо, вращающееся вокруг вертикальной оси (рис. 5.14, слева). В этом случае момент импульса системы человек и платформа-колесо определяется только моментом импульса колеса:

здесь J ч - момент инерции человека и платформы; J K и ω κ - момент инерции и угловая скорость колеса. Так как момент внешних сил относительно вертикальной оси равен нулю, то L сохраняется (L = const).

Если экспериментатор повернет ось вращения колеса на 180° (рис. 5.14, справа), то момент импульса колеса будет направлен противоположно первоначальному и равен J K ω K . Так как вектор момента импульса колеса изменяется, а момент импульса системы сохраняется, то неизбежно должен измениться и момент импульса, человека и платформы, он уже не будет равен нулю 1 . Момент импульса системы в этом случае

1 Небольшим несовпадением оси колеса с осью вращения платформы можно пренебречь.

По формуле (5.42) можно приближенно оценить момент инерции тела человека вместе с платформой, для чего необходимо измерить ω κ , ω 4 и найти J k . Способ измерения угловых скоростей равномерного вращения известен читателю. Зная массу колеса и предполагая, что в основном масса распределена по ободу, по формуле (5.22) можно определить J k . Для уменьшения ошибки можно утяжелить обод велосипедного колеса, проложив по нему специальные шины. Человек должен располагаться симметрично оси вращения.

Более простой вариант рассмотренной демонстрации состоит в том, что человек, стоящий на скамье Жуковского, сам приводит во вращение колесо, которое он держит на вертикальной оси. При этом человек и платформа начинают вращаться в противоположные стороны (рис. 5.15).

5.4. ПОНЯТИЕ О СВОБОДНЫХ ОСЯХ ВРАЩЕНИЯ

Тело, вращающееся вокруг фиксированной оси, в общем случае действует на подшипники или другие устройства, которые сохраняют неизменным положение этой оси. При больших угловых скоростях и моментах инерции эти воздействия могут быть значительными. Однако в любом теле можно выбрать такие оси, направление которых при вращении будет сохраняться без каких-либо специальных устройств. Чтобы понять, какому условию должен удовлетворять выбор таких осей, рассмотрим следующий пример.

Сопоставляя (5.43) с координатами центра масс, замечаем, что силы, действующие на ось, уравновешиваются, если ось вращения проходит через центр масс.

Таким образом, если ось вращения проходит перпендикулярно стержню через центр масс, то воздействия на эту ось со стороны вращающегося тела не будет. Если при этом убрать подшипники, то ось вращения начнет перемещаться, сохраняя неизменным положение в пространстве, а тело будет продолжать вращение вокруг этой оси.

Оси вращения, которые без специального закрепления сохраняют свое направление в пространстве, называют свободными. Примерами таких осей являются оси вращения Земли и волчка, ось всякого брошенного и свободно вращающегося тела и т.п.

У тела произвольной формы всегда имеется по крайней мере три взаимно перпендикулярные оси, проходящие через центр масс, которые могут быть свободными осями вращения. Эти оси называют главными осями инерции. Хотя все три главные оси инерции являются свободными, наиболее устойчивым будет вращение вокруг оси с наибольшим моментом инерции. Дело в том, что в результате неизбежного действия внешних сил, например трения, а также в связи с тем, что трудно задать вращение точно вокруг определенной оси, вращение вокруг остальных свободных осей неустойчиво.

В некоторых случаях, когда тело вращается около свободной оси с малым моментом инерции, оно само изменяет эту ось на ось с наибольшим моментом.

Это явление демонстрируют следующим опытом. К электродвигателю подвешена на нити цилиндрическая палочка, которая может вращаться вокруг своей геометрической оси (рис. 5.17, а). Момент инерции относительно этой оси J 1 = тR 2 /2. При достаточно большой угловой скорости палочка изменит свое положение (рис. 5.17, б). Момент инерции относительно новой оси равен J 2 = ml 2 /12. Если l 2 >6R 2 , то и J 2 > J 1 . Вращение вокруг новой оси будет устойчивым.

Читатель может самостоятельно на опыте убедиться, что вращение брошенной спичечной коробки устойчиво относительно оси, проходящей перпендикулярно большей грани, и неустойчиво или менее устойчиво относительно осей, проходящих перпендикулярно другим граням (см. рис. 5.8).

Вращение животных и человека в свободном полете и при различных прыжках происходит вокруг свободных осей с наибольшим или наименьшим моментом инерции. Так как положение центра масс зависит от позы тела, то при разных позах будут и различные свободные оси.

5.5. ПОНЯТИЕ О СТЕПЕНЯХ СВОБОДЫ

Положение свободной материальной точки в пространстве задается тремя независимыми координатами: х, у, z. Если точка не свободна, а перемещается, например, по некоторой поверхности, то не все три координаты будут независимыми.

Независимые переменные, характеризующие положение механической системы, называют степенями свободы.

У свободной материальной точки три степени свободы, в рассмотренном примере - две степени свободы. Так как молекулу одноатомного газа можно рассматривать как материальную точку, следовательно, такая свободная молекула тоже имеет три степени свободы.

Еще некоторые примеры.

Две материальные точки 1 и 2 жестко связаны друг с другом. Положение обеих точек задано шестью координатами x 1 , y 1 , z 1 , x 2 , y 2 , z 2 , на которые наложены одно ограничение и одна связь, математически выражаемая в форме уравнения:

Физически это означает, что расстояние между материальными точками всегда l. В этом случае число степеней свободы равно 5. Рассмотренный пример является моделью двухатомной молекулы.

Три материальные точки 1, 2 и 3 жестко связаны друг с. другом. Девять координат характеризуют положение такой системы: x 1 , y 1 , z 1 , x 2 , y 2 , z 2 , x 3 , y 3 , z 3 . Однако три связи между точками обусловливают независимость только шести координат. Система имеет шесть степеней свободы. Так как положение трех точек, не лежащих на одной прямой, однозначно определяет положение твердого тела, то и твердое тело имеет шесть степеней свободы.

Такое же число степеней свободы (шесть) имеют трехатомные и многоатомные молекулы, если эти молекулы рассматривать как жесткие образования.

1 Если для зависимой координаты из (5.44) получают мнимую величину, это означает, что выбранные независимые координаты не соответствуют каким-либо точкам, расположенным на сфере заданного радиуса.

В реальных многоатомных молекулах атомы находятся в колебательных движениях, поэтому число степеней свободы таких молекул более шести.

Число степеней свободы определяет не только число независимых переменных, характеризующих положение механической системы, но и, что очень важно, число независимых перемещений системы. Так, три степени свободы свободной материальной точки означают, что любое перемещение точки можно разложить на независимые перемещения по трем осям координат. Так как точка не имеет размеров, то говорить о ее вращении не имеет смысла. Итак, материальная точка имеет три степени свободы поступательного движения. Материальная точка на плоскости, сфере или иной поверхности имеет две степени свободы поступательного движения. Перемещение материальной точки вдоль кривой (условный пример - движение поезда по рельсам) соответствует одной степени свободы поступательного движения.

Твердое тело, вращающееся вокруг неподвижной оси, имеет одну степень свободы вращательного движения. Колесо поезда имеет две степени свободы: одна - вращательного движения, а другая - поступательного (перемещение оси колеса вдоль рельса). Шесть степеней свободы твердого тела означают, что любое перемещение этого тела можно разложить на составляющие: перемещение центра масс раскладывается на три поступательных движения по осям координат, а вращение состоит из трех более простых поворотов относительно осей координат, проходящих через центр масс.

На рис. 5.18-5.20 показаны шарнирные соединения, соответствующие одной, двум и трем степеням свободы.

Рис. 5.18

Рис. 5.19

Рис. 5.20

5.6. ЦЕНТРИФУГИРОВАНИЕ

Центрифугированием называется процесс разделения (сепарации) неоднородных систем, например частиц от жидкостей, в которых они находятся, обусловленный их вращением.

Рассмотрим разделение неоднородных систем в поле силы тяжести. Предположим, что имеется водная суспензия частиц различной плотности. Со временем благодаря действию силы тяжести и выталкивающей силы F A происходит расслаивание частиц: частицы с большей, чем у воды, плотностью тонут, частицы с меньшей, чем у воды, плотностью всплывают. Результирующая сила, действующая, например, на более плотную отдельную частицу, равна:

где ρ 1 - плотность вещества частицы; ρ - плотность воды; V - объем частицы.

Если значения ρ 1 и ρ мало отличаются друг от друга, то сила F p мала и расслоение (осаждение) происходит достаточно медленно. В центрифуге (сепараторе) такое разделение производят принудительно, вращая разделяемую среду.

Рассмотрим физику этого явления.

Пусть рабочий объем центрифуги (рис. 5.21: а - внешний вид; б - схема рабочего объема) полностью занят какой-либо однородной жидкостью. Выделим мысленно небольшой объем V этой жидкости, находящийся на расстоянии r от оси вращения OO". При равномерном вращении центрифуги на выделенный объем кроме силы тяжести и выталкивающей силы, которые уравновешивают друг друга, действует центростремительная сила. Это сила со стороны окружающей объем жидкости. Она, естественно, направлена к оси вращения и равна:

где ρ - плотность жидкости.

Предположим теперь, что выделенный объем V - это сепарируемая частица, плотность вещества которой ρ 1 (ρ 1 Φ ρ). Сила, действующая на частицу со стороны окружающей жидкости, не изменится, как это видно из формулы (5.45).

Для того чтобы частица вращалась вместе с жидкостью, на нее должна действовать центростремительная сила, равная:

где m 1 - масса частицы, а ρ 1 - соответствующая ей плотность.

Рис. 5.21

Если F > F 1 , то частица перемещается к оси вращения. Если F < F 1 , то воздействия на частицу со стороны жидкости будет недостаточно, чтобы удержать ее на круговой траектории, и частица по инерции начнет перемещаться к периферии. Эффект сепарации определяется превышением силы F, действующей со стороны жидкости на выделенную частицу, над тем значением центростремительной силы F 1 , которое обусловливает движение по окружности:

Это выражение показывает, что эффект центрифугирования тем больше, чем больше различие плотностей сепарируемых частиц и жидкости, а также существенно зависит от угловой скорости вращения 1 .

Сравним разделение центрифугированием с разделением с помощью силы тяжести:

1 Сила тяжести и выталкивающая сила при выводе формулы (5.47) не учитываются, так как они направлены вдоль оси вращения и не оказывают принципиального влияния на центрифугирование.

Ультрацентрифуги способны разделить частицы размером менее 100 нм, взвешенные или растворенные в жидкости. Они нашли широкое применение в медико-биологических исследованиях для разделения биополимеров, вирусов и субклеточных частиц.

Быстрота сепарации особенно важна в биологических и биофизических исследованиях, так как со временем может существенно измениться состояние изучаемых объектов.

В этой статье описывается важный раздел физики - "Кинематика и динамика вращательного движения".

Основные понятия кинематики вращательного движения

Вращательным движением материальной точки вокруг неподвижной оси называют такое движение, траекторией которого является окружность, находящаяся в плоскости перпендикулярной к оси, а центр ее лежит на оси вращения.

Вращательное движение твердого тела - это движение, при котором по концентрическим (центры которых лежат на одной оси) окружностям движутся все точки тела в соответствии с правилом для вращательного движения материальной точки.

Пусть произвольное твердое тело T совершает вращения вокруг оси O, которая перпендикулярна плоскости рисунка. Выберем на данном теле точку M. При вращении эта точка будет описывать вокруг оси O круг радиусом r .

Через некоторое время радиус повернется относительно исходного положения на угол Δφ.

За положительное направление поворота принято направление правого винта (по часовой стрелке). Изменение угла поворота со временем называется уравнением вращательного движения твердого тела:

φ = φ(t).

Если φ измерять в радианах (1 рад - это угол, соответствующий дуге, длиной равной ее радиусу), то длина дуги окружности ΔS, которую пройдет материальная точка M за время Δt, равна:

ΔS = Δφr.

Основные элементы кинематики равномерного вращательного движения

Мерой перемещения материальной точки за небольшой промежуток времени dt служит вектор элементарного поворота dφ .

Угловая скорость материальной точки или тела - это физическая величина, которая определяется отношением вектора элементарного поворота к продолжительности этого поворота. Направление вектора можно определить правилом правого винта вдоль оси О. В скалярном виде:

ω = dφ/dt.

Если ω = dφ/dt = const, то такое движение называется равномерное вращательное движение. При нем угловую скорость определяют по формуле

ω = φ/t.

Согласно предварительной формуле размерность угловой скорости

[ω] = 1 рад/с.

Равномерное вращательное движение тела можно описать периодом вращения. Период вращения T - физическая величина, определяющая время, за которое тело вокруг оси вращения выполняет один полный оборот ([T] = 1 с). Если в формуле для угловой скорости принять t = T, φ = 2 π (полный один оборот радиуса r), то

ω = 2π/T,

поэтому период вращения определим следующим образом:

T = 2π/ω.

Число оборотов, которое за единицу времени совершает тело, называется частотой вращения ν, которая равна:

ν = 1/T.

Единицы измерения частоты: [ν]= 1/c = 1 c -1 = 1 Гц.

Сравнивая формулы для угловой скорости и частоты вращения, получим выражение, связывающее эти величины:

ω = 2πν.

Основные элементы кинематики неравномерного вращательного движения

Неравномерное вращательное движение твердого тела или материальной точки вокруг неподвижной оси характеризует его угловая скорость, которая изменяется со временем.

Вектор ε , характеризующий скорость изменения угловой скорости, называется вектором углового ускорения:

ε = dω/dt.

Если тело вращается, ускоряясь, то есть dω/dt > 0 , вектор имеет направление вдоль оси в ту же сторону, что и ω.

Если вращательное движение замедлено - dω/dt < 0 , то векторы ε и ω противоположно направлены.

Замечание . Когда происходит неравномерное вращательное движение, вектор ω может меняться не только по величине, но и по направлению (при повороте оси вращения).

Связь величин, характеризующих поступательное и вращательное движение

Известно, что длина дуги с углом поворота радиуса и его величиной связана соотношением

ΔS = Δφ r.

Тогда линейная скорость материальной точки, выполняющей вращательное движение

υ = ΔS/Δt = Δφr/Δt = ωr.

Нормальное ускорение материальной точки, что выполняет вращательно поступательное движение, определим следующим образом:

a = υ 2 /r = ω 2 r 2 /r.

Итак, в скалярном виде

a = ω 2 r.

Тангенциальное ускоренной материальной точки, которая выполняет вращательное движение

a = ε r.

Момент импульса материальной точки

Векторное произведение радиуса-вектора траектории материальной точки массой m i на ее импульс называется моментом импульса этой точки касательно оси вращения. Направление вектора можно определить, воспользовавшись правилом правого винта.

Момент импульса материальной точки (L i ) направлен перпендикулярно плоскости, проведенной через r i и υ i , и образует с ними правую тройку векторов (то есть при движении с конца вектора r i к υ i правый винт покажет направление вектора L i).

В скалярной форме

L = m i υ i r i sin(υ i , r i).

Учитывая, что при движении по кругу радиус-вектор и вектор линейной скорости для i-й материальной точки взаимно перпендикулярные,

sin(υ i , r i) = 1.

Так что момент импульса материальной точки для вращательного движения примет вид

L = m i υ i r i .

Момент силы, которая действует на i-ю материальную точку

Векторное произведение радиуса-вектора, который проведен в точку приложения силы, на эту силу называется моментом силы, действующей на i-ю материальную точку относительно оси вращения.

В скалярной форме

M i = r i F i sin(r i , F i).

Считая, что r i sinα = l i , M i = l i F i .

Величина l i , равная длине перпендикуляра, опущенного из точки вращения на направление действия силы, называется плечом силы F i .

Динамика вращательного движения

Уравнение динамики вращательного движения записывается так:

M = dL/dt.

Формулировка закона следующая: скорость изменения момента импульса тела, которое совершает вращение вокруг неподвижной оси, равна результирующему моменту относительно этой оси всех внешних сил, приложенных к телу.

Момент импульса и момент инерции

Известно, что для i-й материальной точки момент импульса в скалярной форме задается формулой

L i = m i υ i r i .

Если вместо линейной скорости подставить ее выражение через угловую:

υ i = ωr i ,

то выражение для момента импульса примет вид

L i = m i r i 2 ω.

Величина I i = m i r i 2 называется моментом инерции относительно оси i-й материальной точки абсолютно твердого тела, проходящей через его центр масс. Тогда момент импульса материальной точки запишем:

L i = I i ω.

Момент импульса абсолютно твердого тела запишем как сумму моментов импульса материальных точек, составляющих данное тело:

L = Iω.

Момент силы и момент инерции

Закон вращательного движения гласит:

M = dL/dt.

Известно, что представить момент импульса тела можно через момент инерции:

L = Iω.

M = Idω/dt.

Учитывая, что угловое ускорение определяется выражением

ε = dω/dt,

получим формулу для момента силы, представленного через момент инерции:

M = Iε.

Замечание. Момент силы считается положительным, если угловое ускорение, которым он вызван, больше нуля, и наоборот.

Теорема Штейнера. Закон сложения моментов инерции

Если ось вращения тела через центр масс его не проходит, то относительно этой оси можно найти его момент инерции по теореме Штейнера:
I = I 0 + ma 2 ,

где I 0 - начальный момент инерции тела; m - масса тела; a - расстояние между осями.

Если система, которая совершает обороты округ неподвижной оси, состоит из n тел, то суммарный момент инерции такого типа системы будет равен сумме моментов, ее составляющих (закон сложения моментов инерции).

Рассмотрим самый простой случай: шарик массой т равномерно движется со скоростьюv 0 вдольрадиуса вращающегося диска. Чтобы обеспечить такое движение снабдим шарикнаправляющимстержнем, по которому он мог бы перемещаться без трения. Нитка, прикрепленная к шарику, позволит ему в радиальном направлении двигаться с постоянной скоростьюv 0 (рис. 5.6).

Рис. 5.6

Диск вращается с угловойскоростью. Опишем движение шарика в неподвижной инерциальной системе отсчётаS (x ,y ). В этой системе движение шарика складывается из двух движений: равномерного прямолинейного - по радиусу диска со скоростьюv 0 и кругового движения с угловой скоростью.

В результате сложения этих двух движений, шарик будет двигаться по криволинейной траектории - разворачивающейся спирали.

В произвольный момент времени t шарик на расстоянииr от оси вращения будет иметь радиальную скоростьv 0 и касательную - тангенциальную скорость, связанную с вращением диска (r ) (рис. 5.7).

Рис. 5.7

Посмотрим, как изменятся эти скорости шарика спустя малое время dt .

Во-первых, вся картина скоростей повернётся на угол d =dt (рис. 5.7 б). Во вторых, радиальная скорость (оставаясь неизменной по величине -V 0) получит приращение:

dV 1 =V 0 d =V 0 dt , (5.5)

связанное с повтором вектора скорости V 0 на уголd =dt .

Изменится и тангенциальная скорость. Её изменение по величине определяется тем, что шарик удалится от оси вращения на расстояние dr =V 0 dt . Поэтому:

dV 2 =(r +dr ) –r =dr =V 0 dt . (5.6)

Кроме того, эта скорость изменится на величину:

dV 3 = rd  = r dt =  2 rdt , (5.7)

в связи с поворотом вектора этой скорости на угол d .

Проанализировав все эти изменения, придём к выводу, что в радиальном направлении изменение скорости составит величину:

dV r =dV 3 = 2 rdt ,

а в тангенциальном:

dV  =dV 1 +dV 2 = 2V 0 dt .

Разделив эти изменения на промежуток времени dt , получим соответствующие компоненты ускорения:

; (5.8)

. (5.9)

Несложно ответить на вопрос: какие силы обеспечивают эти ускорения?

Центростремительное ускорение создаётся упругой силой натяжения нити (F ц.с. =F упр. =ma ц.с. =m  2 r ), направленной по радиусу к оси вращения. Касательное ускорениеa  поддерживается упругой силой деформированного стержня (
=ma  =m 2V 0). Стержень при движении прогибается и действует на шарик с силой, направленной в сторону вращения (рис. 5.8).

Рис. 5.8

Запишем уравнения движения шарика в инерциальной системе отсчёта. Это уравнения второго закона Ньютона для двух движений - вдоль радиуса:

, (5.10)

и в перпендикулярном направлении:

. (5.11)

Теперь посмотрим, как представляется движение этого же шарика наблюдателю, вращающемуся вместе с диском.

Этот наблюдатель видит, что шарик в его вращающейся системе отсчёта движется равномерно и прямолинейно со скоростью =сonst вдоль радиуса диска. Ускорение шарика равно нулю, но при этом на него действует упругая сила натяжения нитиF ц.с. =m  2 r и упругая сила деформированного стержняF =m 2V 0 . Их равнодействующая никак не может быть равна нулю.

Для того, чтобы записать уравнение движения этого тела в неинерциальной системе отсчёта в виде уравнений второго закона Ньютона, к реально действующим упругим силам прибавим две силы инерции (рис. 5.9):

(5.12)

. (5.13)

Рис. 5.9

Теперь и в радиальном и в тангенциальном направлениях суммы сил будут равны нулю, что и объясняет равномерное движение шарика вдоль радиуса.

С первой из сил инерции
мы знакомы. Это центробежная сила инерции.

Вторая сила инерции
называется силой Кориолиса.

Эти силы можно записать в векторном виде:

.

Подводя итог рассмотрению движений в неинерциальных системах отсчёта, отметим следующие основные моменты.

Ньютоновским уравнением движения можно воспользоваться и в неинерциальных системах отсчёта. Но при этом систему реально действующих сил нужно дополнить силами инерции.

В неинерциальной системе отсчёта, движущейся прямолинейно и поступательно с ускорением , сила инерции равна:

. (5.14)

В неинерциальной системе отсчёта, вращающейся с угловой скоростью , в общем случае следует ввести две силы инерции:

центробежную
, (5.15)

и кориолисову
. (5.16)

На тело действуют три силы:
сила тяжести m , сила реакции опоры и сила трения тр.

В инерциальной системе отсчета, связанной с Землей, второй закон Ньютона будет иметь вид:

Движение тела относительно Земли представляет собой движение в горизонтальной плоскости по окружности радиусом R. Силы, действующие на него в вертикальном направлении, скомпенсированы. Вектор ускорения лежит в горизонтальной плоскости, а само ускорение является центростремительным. Его величина определяется формулой:

Проецирование векторного уравнения на координатные оси X и Y дает два скалярных уравнения:


Первое уравнение показывает, что в роли центростремительной силы выступает сила трения, второе — констатирует, что вертикальные силы взаимно уравновешены.

Сила трения покоя подчиняется неравенству:

поэтому при